Transformation de FOURRIER discrète

Définition de la transformée de Fourrier des signaux numériques

x(k) → X(f)

X(f) est périodiques de période 1. En général c'est une fonction complexe de la variable f. f est une variable continue, f est une fréquence de moins l'infini à plus l'infini.
La transformée de Fourrier de x(k) est notée:

Et la relation inverse s'écrit:

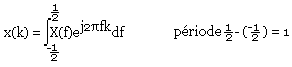
Remarque:

Nous notons deux difficultés associées à cette définition.

• La première difficulté est liée à la nature continue de la variable ƒ, ceci n'est pas commode dans un système de traitement numérique
• Deuxième difficulté est liée au nombre infini d'échantillon, ce qui n'est pas le cas des signaux utilisés dans la réalité.

Proposition de solution: Il faut discrétiser la variable f et limiter le nombre d'échantillon.

---

Transformée de FOURRIER discrète

Description de la variable ƒ

Nous remplaçons la variable ƒ, par une autre variable ƒ_n.
Incrémentation : C'est une augmentation par pas ou par sont constant.
ƒ_n est appelé fréquence harmonique de la transformée de Fourrier discret comme X(ƒ) est période , il suffit d'utiliser une seule période. On peut diviser cette période en n incrémentations comme X(t) est périodique. Ce qui donne:

Conséquence de la discrétisation

Compte tenu du changement de variable, la transformée de FOURRIER inverse s'écrit:

Quelques propriétés de W_N^nk:

W_N^h+l = W_N^k+l=W_N^h-W_N^l (Séparabilité)
W_N^k+lw = W_N^k = W_N^{k module N}

Valeurs spatiales:

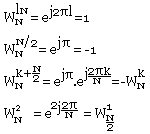
Transformée de FOURRIER discrète des signaux périodiques de période N

En ne considérant que la période allant de 0 à N-1

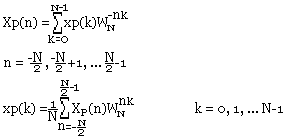
Transformée de FOURRIER à signaux réels : signaux à durée limitée

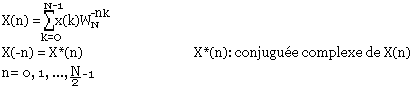
Remarque:

Si N est impair on prendra la valeur entière de N/2. X(n) est périodique de période N.

Démonstration:

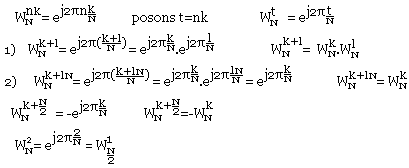
Exercice 1:

Qu'elle est la transformée de FOURRIER du signal suivant:

x(k) = a^kε(k) avec a : réel
discutez de l'existence de la transformée en fonction de a.

Exercice 2:

Qu'elle est le signal donc la transformée de FOURRIER est x(f-f₀) ou f₀ est une constante.